Graficas del COVID
Durante el periodo de confinamiento -el de teletrabajo todavía está activo- los miembros de Kampal hemos organizado distintas actividades y proyectos laterales: los webinars, la página de radios de 1 km, medidas de actividad en twitter, ayudar con los datos provinciales de numeroteca,… y naturalmente hacer nuestras propias gráficas y tablas de excel, como muchos de los científicos e ingenieros confinados.
No corresponde a esta entrada de blog hablar de posibles modelos de la epidemia, y aunque los esté usando para guiar los ajustes de las gráficas lo que me interesa es hablar propiamente de los distintos tipos de visualización. Una cosa que me ha llamado la atención respecto a las informaciones que se han ido publicando en los medios sociales ha sido el énfasis en el eje temporal. Quizás por afectarnos directamente los días. Pero este tipo de gráficas no son las más informativas, porque contienen términos exponenciales, tanto crecientes como decrecientes, que hacen difícil estimar hacia donde van las cantidades absolutas.
Una técnica más del gusto de los físicos a la hora de dibujar un movimiento es hacerlo en el llamado espacio de fase, o fibrado cotangente, donde se pinta momento y posición. O en el fibrado tangente, el espacio de velocidades y posiciones, a veces llamado «de configuración». En general, los modelistas que trabajan con ecuaciones diferenciales de primer orden llaman «espacio de fase» al que corresponde a los valores de toda la tupla de ecuaciones. En todas estas representaciones un punto indica todos los valores que hacen falta para fijar una trayectoria, así que todas las trayectorias que pintemos en estos espacios irán moviéndose sin intersectar. O si intersectan, es que hay más parámetros en juego y solo estamos viendo una proyección.
¿Qué forma tienen estas curvas? En particular me interesa el espacio de velocidades y posiciones. Considerad la ecuación diferencial de una curva logistica, ![]() . La imagen en el eje temporal es la tipica «S» o «escalón» creciendo desde cero hasta
. La imagen en el eje temporal es la tipica «S» o «escalón» creciendo desde cero hasta ![]() . Pero la imagen en el plano
. Pero la imagen en el plano ![]() será una parábola cortando los ejes en cero y en
será una parábola cortando los ejes en cero y en ![]() . Podemos tomar los datos diarios de una curva, aproximar
. Podemos tomar los datos diarios de una curva, aproximar ![]() , y pintar esa grafica, y de ahi extraer una vision de como se esta comportando el sistema. Incluso en curvas exponenciales, como
, y pintar esa grafica, y de ahi extraer una vision de como se esta comportando el sistema. Incluso en curvas exponenciales, como ![]() o
o ![]() , dibujar el espacio de «velocidad en cada punto del recorrido» nos permite ver los coeficientes de la exponencial sin recurrir al papel semilogaritmico. Eso es lo que esta haciendo por ejemplo Stuart Alan Kauffman en la fotografia que muestra esta entrevista (y en el minuto 5 de este video). En la internet solamente he encontrado un sitio web que pinta las graficas de «velocidad en cada punto» para todos los paises.
, dibujar el espacio de «velocidad en cada punto del recorrido» nos permite ver los coeficientes de la exponencial sin recurrir al papel semilogaritmico. Eso es lo que esta haciendo por ejemplo Stuart Alan Kauffman en la fotografia que muestra esta entrevista (y en el minuto 5 de este video). En la internet solamente he encontrado un sitio web que pinta las graficas de «velocidad en cada punto» para todos los paises.
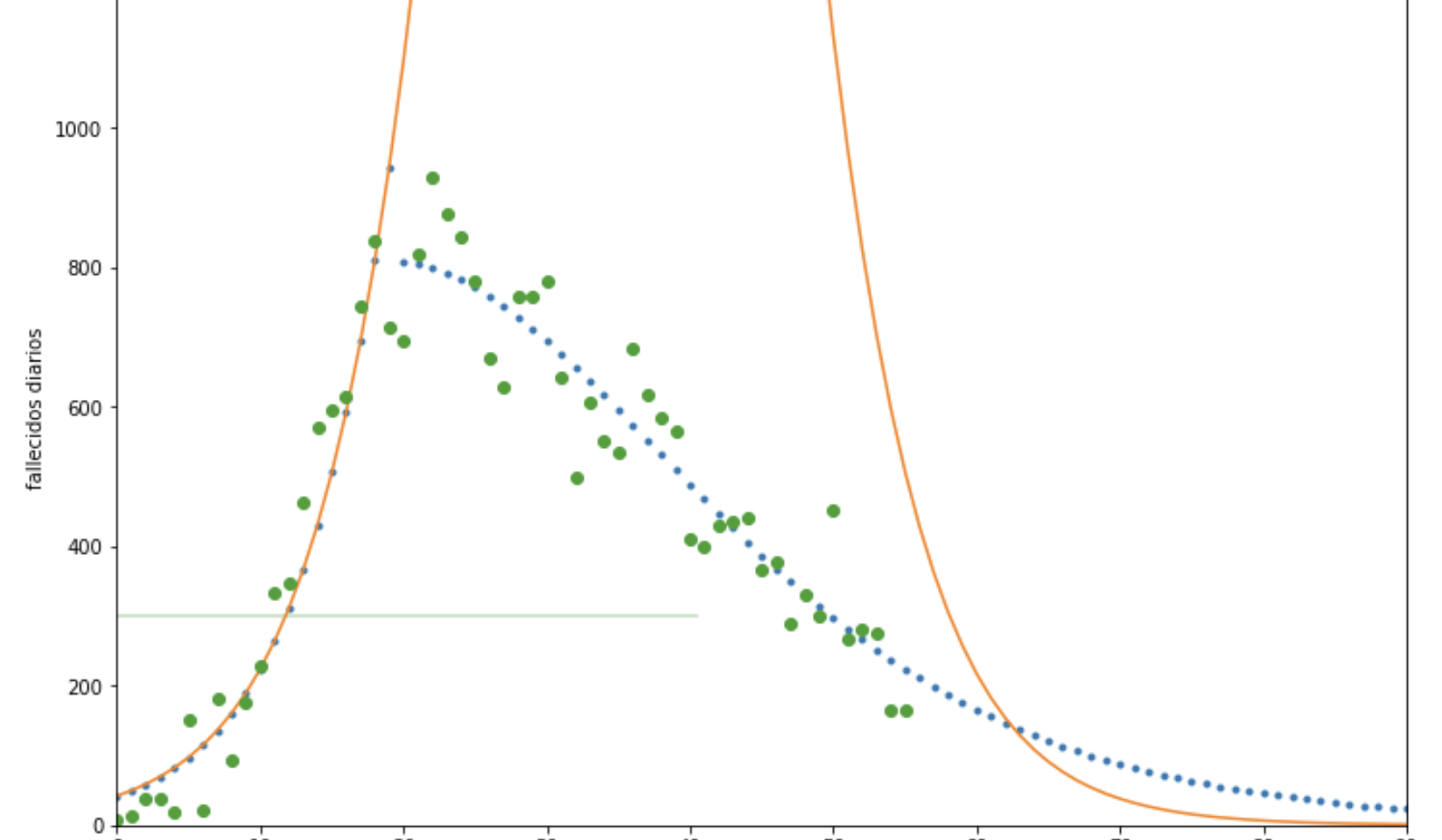
Pongo un ejemplo concreto: descarguemos la tabla de fallecimientos nacional del dia de hoy y pintamos por un lado el acumulado en funcion del tiempo, por otro la variacion diaria bien en funcion del tiempo, bien en funcion del acumulado. Cada una nos da diferentes mensajes. En la cabecera del post hemos puesto la variacion diaria en funcion del tiempo, que nos permite hacernos una idea del comportamiento general, aunque seguramente en la fase final tenga procesos de tamaño finito dificiles de tener en cuenta: no se puede contagiar a media persona.
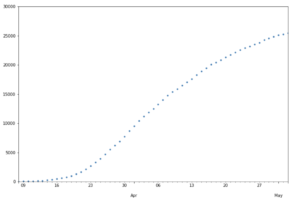
Para estimar cual va a ser el total de contagiados, o de fallecidos, tenemos dos opciones:
- la curva acumulada «en el tiempo»
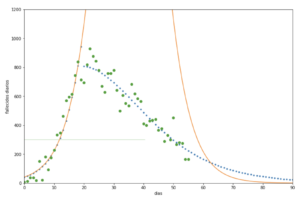
- o la curva «en un espacio de fase»
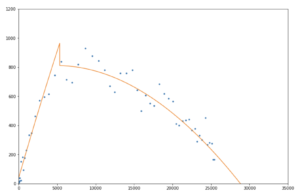
Eje vertical: fallecimientos diarios. Eje horizontal: fallecimentos totales. La linea naranja es un fit tipo SIR.
Aunque no hubieramos añadido un fit como guia visual, el plot en el «espacio de fase» nos permite determinar hacia donde va el resultado total de forma mucho menos confusa que el plot «en el tiempo». Por supuesto, podriamos intentar añadir un fit exacto tambien en el tiempo, pero es necesario tener el modelo bastante claro dado que ya no hay ya una curva puramente logistica y ni siquiera esta claro que estemos ya en el regimen de aproximacion exponencial (que como hemos implicado en parrafos anteriores deberia corresponder a una recta).
¿Qué ocurre matematicamente para que no tengamos una parabola? Podriamos esperar que el acumulado de fallecimientos fuera una representacion retrasada 14 o 15 dias del acumulado de contagios (5.2 dias de incubacion + 10 dias de evolucion de la enfermedad), pero ni siquera este es una curva logistica dado que hay recuperaciones de la enfermedad. Mas bien hay que pensar que los infectados totales cumpliran
![]()
y en los modelos más simples los «activos» ya no coinciden con los infectados totales; difieren en una correccion logaritmica que afortunadamente añade un nuevo cero a la ecuacion, y crea la famosa «Inmunidad de grupo» incluso en poblaciones bien mezcladas. Lamentablemente aquí nuestro cero viene forzado por los parametros de confinamiento, y si bien indica la capacidad de controlar la epidemia, no nos deja exentos de nuevas olas.
Si te interesan detalles más concretos sobre modelado, te recomiendo la grabación del webinar de Yamir Moreno hace unos días. Y si quieres intentar simulaciones, puedes encontrar varias páginas web online que otros confinados han ido haciendo, en particular te recomiendo esta pagina reciente, bastante detallada.